- What is a flow network
The topologies of real-world networks have been extensively studied, but their flow structures have not attracted enough attention. In flow structures we focus on the directed, long-distance interactions between nodes and communities, which have strong applied meanings but are rarely covered by previous network studies.
The following figure shows a flow network as an aggrenation of several streams. In our data set, a stream is generated when a users of stackoverflow.com answer a series of questions sequentially, so the flow structure shows the collective behavior of users in answering questions. Here is our data set:
user: 26624, time: 03:40:31, Question ID: 1983425
user: 89771, time: 22:53:24, Question ID: 1989888
user: 57348, time: 04:47:02, Question ID: 1987883
user: 14343, time: 18:42:11, Question ID: 1989251
user: 20489, time: 23:43:40, Question ID: 1987833
user: 24587, time: 11:18:05, Question ID: 1988359
user: 8206, time: 07:42:38, Question ID: 1988127
user: 8206, time: 07:48:49, Question ID: 1988091
user: 8206, time: 08:13:45, Question ID: 1988160
user: 8206, time: 08:45:35, Question ID: 1988196
user: 8206, time: 09:42:33, Question ID: 1988248
user: 8206, time: 13:54:18, Question ID: 1988642
user: 8206, time: 14:20:06, Question ID: 1988665
user: 8206, time: 14:34:48, Question ID: 1988728
user: 35501, time: 08:00:43, Question ID: 1988049
user: 165905, time: 19:23:57, Question ID: 1989255
user: 79891, time: 12:23:36, Question ID: 1980082
To study a flow network we shoud make sure it satistifies the “flow equivalence” condition. As shown in the attached figure, we add two artificial nodes, “soruce” and “sink”, to balance the network such that inflow (the sum of weighted indegree) equals outflow (the sum of weighted indegree) on every node within the network.
To construct and balance a flow network from individual records (the time variable in the data set should be removed first) we use the following python scripts:
import networkx as nx
import re
from numpy import linalg as LA
import numpy as np
from collections import defaultdict
from os import listdir
from os.path import isfile, join
import matplotlib.pyplot as plt
def constructFlowNetwork (C):
E=defaultdict(lambda:0)
E[('source',C[0][1])]+=1
E[(C[-1][1],'sink')]+=1
F=zip(C[:-1],C[1:])
for i in F:
if i[0][0]==i[1][0]:
E[(i[0][1],i[1][1])]+=1
else:
E[(i[0][1],'sink')]+=1
E[('source',i[1][1])]+=1
G=nx.DiGraph()
for i,j in E.items():
x,y=i
G.add_edge(x,y,weight=j)
return G
def flowBalancing(G):
RG = G.reverse()
H = G.copy()
def nodeBalancing(node):
outw=0
for i in G.edges(node):
outw+=G[i[0]][i[1]].values()[0]
inw=0
for i in RG.edges(node):
inw+=RG[i[0]][i[1]].values()[0]
deltaflow=inw-outw
if deltaflow > 0:
H.add_edge(node, "sink",weight=deltaflow)
elif deltaflow < 0:
H.add_edge("source", node, weight=abs(deltaflow))
else:
pass
for i in G.nodes():
nodeBalancing(i)
if ("source", "source") in H.edges(): H.remove_edge("source", "source")
if ("sink", "sink") in H.edges(): H.remove_edge("sink", "sink")
return H
def outflow(G,node):
n=0
for i in G.edges(node):
n+=G[i[0]][i[1]].values()[0]
return n
By applying the above scripts we obtain the weighted, directed flow network as an edge list:
1988160->1988196: 1
1983425->sink: 1
1988642->1988665: 1
1989251->sink: 1
1988196->1988248: 1
1989255->sink: 1
1988359->sink: 1
1989888->sink: 1
1988049->sink: 1
source->1989888: 1
source->1983425: 1
source->1989251: 1
source->1988359: 1
source->1989255: 1
source->1988049: 1
source->1980082: 1
source->1987883: 1
source->1987833: 1
source->1988127: 1
1980082->sink: 1
1987883->sink: 1
1988728->sink: 1
1988665->1988728: 1
1988248->1988642: 1
1987833->sink: 1
1988091->1988160: 1
1988127->1988091: 1
On this balanced flow network we can calculate the network inflow from “source” (which equals the network outflow to “sink”) as 10. This is also the number of individual streams (individual users). The network total flow is 27, which is also the total numbers of answers. Dividing 27 by 10 we get 2.7, this is the average flow length of the network (the number of questions answered by an average user in the system).
Now, a particularly interesting question is, given this flow network structure, can we retrive individual ctreams ? This idea sounds crazy, but it is not entirely impossible. I found that by using the Dijkstra algorithm recursively it is possible to do this. The Dijkstra algorithm is designed for finding the shortest path between two nodes in a graph:
def Dijkstra(G,target):
# initialize
RG = G.reverse()
dist = {}
previous = {}
for v in RG.nodes():
dist[v] = float('inf')
previous[v] = 'none'
dist[target] = 0
u = target
# main loop
while u!='source' and dist:
u = min(dist, key=dist.get)
distu = dist[u]
del dist[u]
for u,v in RG.edges(u):
if v in dist:
alt = distu + RG[u][v]['weight']
if alt < dist[v]:
dist[v] = alt
previous[v] = u
#retrieve flow
path=('source',)
last='source'
while last!=target:
if last in previous:
nxt = previous[last]
path += (nxt,)
last = nxt
return path
By applying the algorithm and adjusting the graph repeatively, we get the following result:
('source', 1980082, 'sink'): 1,
('source', 1983425, 'sink'): 1,
('source', 1987833, 'sink'): 1,
('source', 1987883, 'sink'): 1,
('source', 1988049, 'sink'): 1,
('source', 1988127, 1988091, 1988160, 1988196, 1988248, 1988642, 1988665, 1988728, 'sink'): 1,
('source', 1988359, 'sink'): 1,
('source', 1989251, 'sink'): 1,
('source', 1989255, 'sink'): 1,
('source', 1989888, 'sink'): 1}
This is amzaing, we successively retrived every single path! But I also found that this method has two limitations.
-
It can not handle loops, this is the limitation of the Dijkstra algorithm itself;
-
Some times different combinations of individual streams lead to the same flow network structure, such as two triangles heading at each other. In these cases the Dijkstra method can not gurantee the retrieved individual streams are all correct.
For example, using the following two different data sets:
E1 = [['user A',0],['user A',1],['user A',2],['user A',3],['user B',2]]
E2 = [['user A',0],['user A',1],['user A',2],['user B',2],['user B',3]]
We get the same flow network:
source->0: 1
0->1: 1
1->2: 1
2->3: 1
3->sink: 1
source->2: 1
2->sink: 1
Despite these limitations, this method is novel and powerful. It is interesting to see its application in other real-world networks.
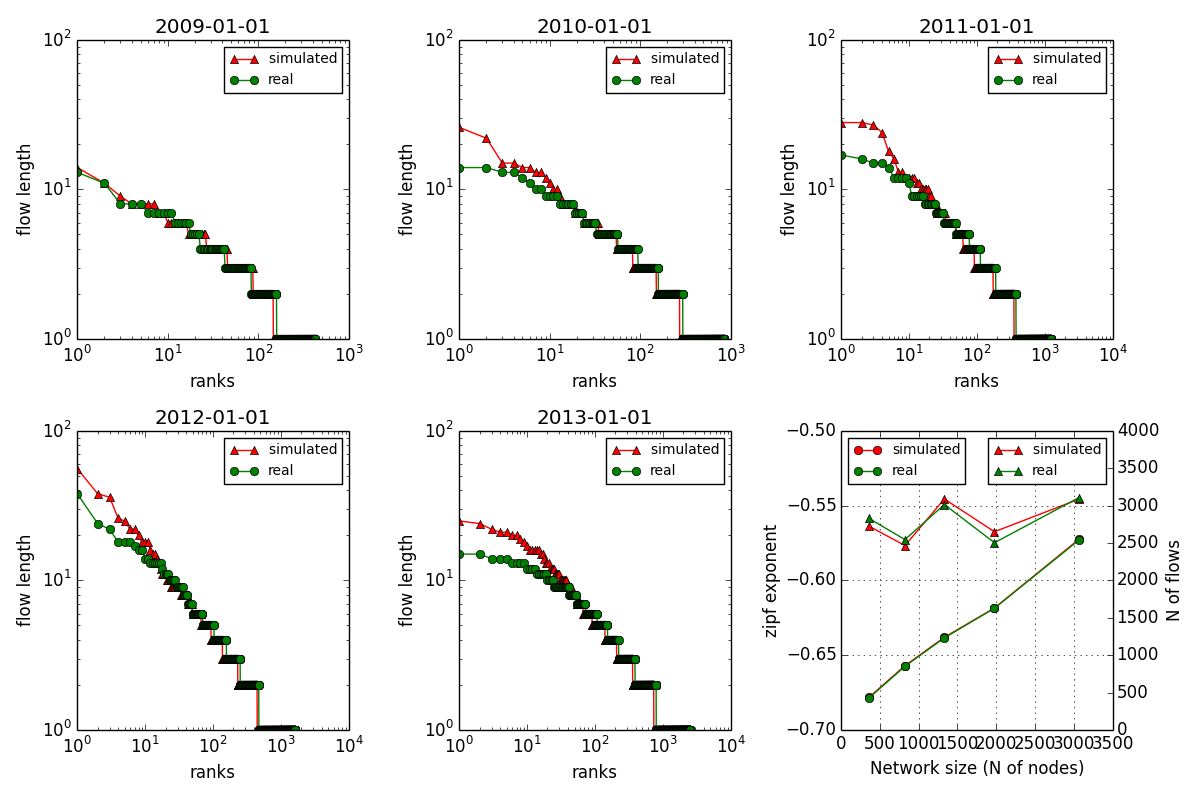
The following figure comapres the length distributions of the real flows (generted from user record) with that of the simulated flows (retrieved from aggregated flow networks using the above mentioned method) using stackoverflow data.