 Figure cited from here
Figure cited from here
What is genertic programming ?
As introduced by Wikipedia, genetic programming (GP) is an evolutionary algorithm-based methodology inspired by biological evolution to find computer programs that perform a user-defined task. Essentially GP is a set of instructions and a fitness function to measure how well a computer has performed a task. It is a specialization of genetic algorithms (GA) where each individual is a computer program.
For example, given the dataset
[[27, 23, 861],
[14, 36, 315],
...
[2, 38, 91]]
The frist two columns are x and y and the third is z, how can we find a function that predicts z from a new pair of x and y? Regression, Artificial Neural Network, …, these are all options. But the genetic programming provides a new possibility.
Programs as parse trees
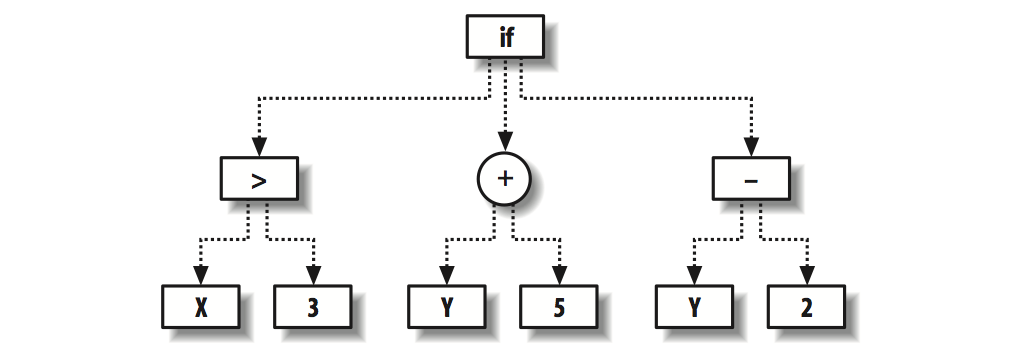
A program is an operation that turns input into output. So basically functions defined by codes and math symbols are the same. A function can be understood as a parse tree, which organize a serious of operations together. The following Python code defines a class that can be used to express parse trees.
from random import random,randint,choice
from copy import deepcopy
from math import log
#classes for parse tree
class fwrapper:
def __init__(self,function,childcount,name):
self.function=function
self.childcount=childcount
self.name=name
class node:
def __init__(self,fw,children):
self.function=fw.function
self.name=fw.name
self.children=children
def evaluate(self,inp):
results=[n.evaluate(inp) for n in self.children]
return self.function(results)
def display(self,indent=0):
print (' '*indent)+self.name
for c in self.children:
c.display(indent+1)
class paramnode:
def __init__(self,idx):
self.idx=idx
def evaluate(self,inp):
return inp[self.idx]
def display(self,indent=0):
print '%sp%d' % (' '*indent,self.idx)
class constnode:
def __init__(self,v):
self.v=v
def evaluate(self,inp):
return self.v
def display(self,indent=0):
print '%s%d' % (' '*indent,self.v)
# construct operations by using fwrapper on functions
addw=fwrapper(lambda l:l[0]+l[1],2,'add')
subw=fwrapper(lambda l:l[0]-l[1],2,'subtract')
mulw=fwrapper(lambda l:l[0]*l[1],2,'multiply')
def iffunc(l):
if l[0]>0: return l[1]
else: return l[2]
ifw=fwrapper(iffunc,3,'if')
def isgreater(l):
if l[0]>l[1]: return 1
else: return 0
gtw=fwrapper(isgreater,2,'isgreater')
flist=[addw,mulw,ifw,gtw,subw]
Using the above code we can define the tree shown in the figue by
# an exmaple tree
def exampletree():
return node(ifw,[
node(gtw,[paramnode(0),constnode(3)]),
node(addw,[paramnode(1),constnode(5)]),
node(subw,[paramnode(1),constnode(2)]),
]
)
and evaluate the tree by
exampletree().evaluate([5,3])
or print the tree by
def display(self,indent=0):
print (' '*indent)+self.name
for c in self.children:
c.display(indent+1)
exampletree().display()
Setting up an example datset
We set up an exmple data set using the following function:
def hiddenfunction(x,y):
return x**2+2*y+3*x+5
def buildhiddenset():
rows=[]
for i in range(100):
x=randint(0,40)
y=randint(0,40)
rows.append([x,y,hiddenfunction(x,y)])
return rows
hiddenset=buildhiddenset()
Genertic evolutions
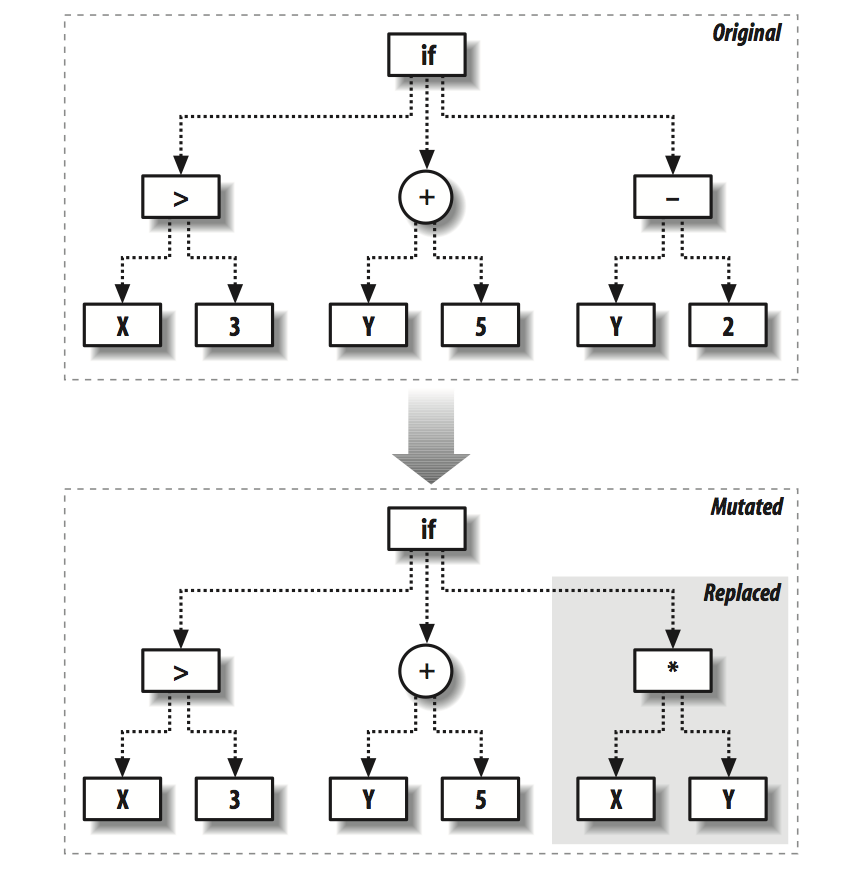
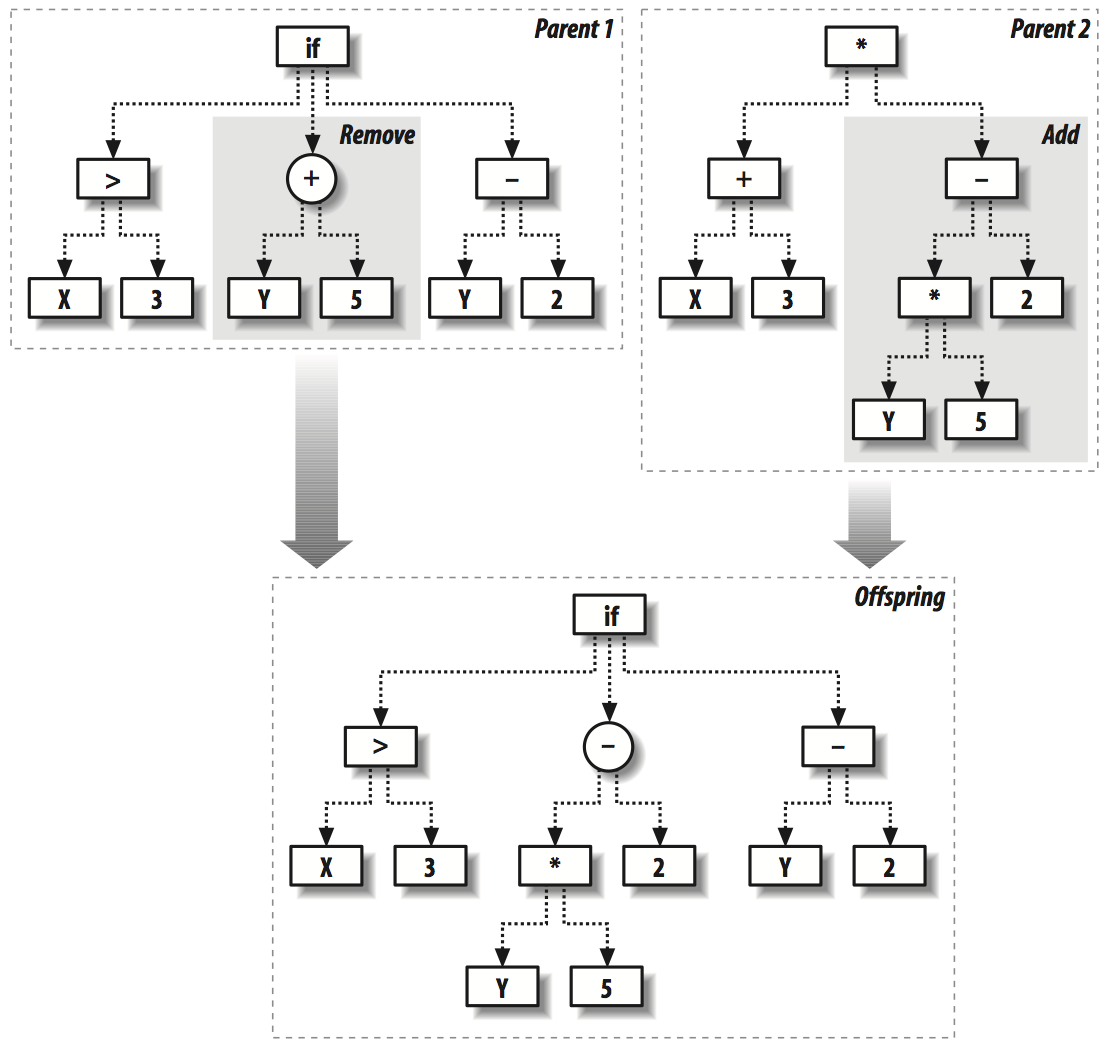
We now define the following functions to simulate the mutation and crossover behavior in nature.
def scorefunction(tree,s):
dif=0
for data in s:
v=tree.evaluate([data[0],data[1]])
dif+=abs(v-data[2])
return dif
#scorefunction(makerandomtree(2),hiddenset)
def mutate(t,pc,probchange=0.1):
if random()<probchange:
return makerandomtree(pc)
else:
result=deepcopy(t)
if isinstance(t,node):
result.children=[mutate(c,pc,probchange) for c in t.children]
return result
#mutate(makerandomtree(2),2).display()
def crossover(t1,t2,probswap=0.7,top=1):
if random()<probswap and not top:
return deepcopy(t2)
else:
result=deepcopy(t1)
if isinstance(t1,node) and isinstance(t2,node):
result.children=[crossover(c,choice(t2.children),probswap,0) for c in t1.children]
return result
#crossover(makerandomtree(2),makerandomtree(2)).display()
Setting up the evolution environment
After we preparing the data set and setting up the mutation and crossover functions we are ready to move on to set up the evironment for evolution, i.e., fitting the data.
def evolve(pc,popsize,rankfunction,maxgen=500,mutationrate=0.1,breedingrate=0.4,pexp=0.7,pnew=0.05):
# Returns a random number, tending towards lower numbers. The lower pexp # is, more lower numbers you will get
def selectindex():
return int(log(random())/log(pexp))
# Create a random initial population
population=[makerandomtree(pc) for i in range(popsize)]
for i in range(maxgen):
scores=rankfunction(population)
print scores[0][0]
if scores[0][0]==0: break
# The two best always make it
newpop=[scores[0][1],scores[1][1]]
# Build the next generation
while len(newpop)<popsize:
if random()>pnew:
newpop.append(mutate(crossover(scores[selectindex( )][1], \
scores[selectindex( )][1],
probswap=breedingrate),
pc,probchange=mutationrate))
else:
# Add a random node to mix things up
newpop.append(makerandomtree(pc))
population=newpop
scores[0][1].display( )
return scores[0][1]
def getrankfunction(dataset):
def rankfunction(population):
scores=[(scorefunction(t,dataset),t) for t in population]
scores.sort( )
return scores
return rankfunction
The reuslt can be obtain by
rf=getrankfunction(buildhiddenset())
evolve(2,500,rf,mutationrate=0.2,breedingrate=0.1,pexp=0.7,pnew=0.1)
The function survived in the data selection
After an evolution that lasted for more than ten minutes (a disadvantage of GP is that it is very time conusming in some cases), we got our result as shown in the following figure. If we do some simple math we will find that it equals to the function we defined above.